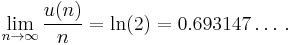Unusual number
In number theory, an unusual number is a natural number n whose largest prime factor is strictly greater than 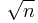 (sequence A064052 in OEIS). All prime numbers are unusual.
(sequence A064052 in OEIS). All prime numbers are unusual.
A k-smooth number has all its prime factors less than or equal to k, therefore, an unusual number is non-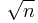 -smooth.
-smooth.
If we denote the number of unusual numbers less than or equal to n by u(n) then u(n) behaves as follows:
| n | u(n) | u(n) / n |
| 10 | 6 | 0.6 |
| 100 | 67 | 0.67 |
| 1000 | 715 | 0.715 |
| 10000 | 7319 | 0.7319 |
| 100000 | 70128 | 0.70128 |
Richard Schroeppel proved in 1972 that the asymptotic probability that a randomly chosen number is unusual is ln(2). In other words:
External links
- Weisstein, Eric W., "Rough Number" from MathWorld.
|
||||||||||||||||||||||